1 Introduction

C-DVM language was designed to support the development of portable and efficient parallel computational applications. The language is an extension of C language according to DVM model developed in Keldysh Institute of Applied Mathematics [1].

Traditionally applications for serial computers were created using Fortran and C languages. At present such applications are created for multiprocessor computers with distributed memory and networks using as a rule Fortran 77 and C extended by message transfer libraries (PVM, MPI). The development of such parallel applications requires from a programmer far more efforts than development of sequential ones, as the programmer has to distribute data and computations between different processors and also provide interaction of processors via message passing. Actually, the parallel application is a system of interacting programs, each program running at its own processor. The programs running at different processors may be either quite different, or may differ a little, or may be the same program whose behavior depends on the processor number. However, even in the last case the programmer is forced to develop and maintain two versions of the program - the sequential and parallel ones.

Using C-DVM language the programmer deals with the only version of the program both for sequential and parallel execution. Besides algorithm description by means of usual C features the program contains rules for parallel execution of the algorithm. These rules are syntactically organized in such a manner that they are "transparent" for standard C compilers at serial computers. Therefore it is possible to execute and to debug the C-DVM program at workstations as a usual sequential one.

Thus the C-DVM language is a standard C language extended by features to describe the rules of parallel program execution. The C-DVM language provides:

• distribution of array elements over the processors;
• distribution of loop iterations over the processors;
• specification of parallel executed program sections (parallel tasks) and their mapping on the processors;
• organization of efficient access to remote data (the data located at other processors);
• organization of efficient execution of reduction operations, that is global operations on the data located at different processors (such as summing values or finding their maximal and minimal values).

To create C-DVM programs the special system of parallel program development automation, named DVM-system, is provided.

DVM-system provides unified toolkit to develop parallel programs of scientific-technical calculations in C and Fortran 77.

DVM parallel model. DVM parallel model is based on data parallel model. The DVM name reflects two names of the model - Distributed Virtual Memory and Distributed Virtual Machine. These two names show that DVM model is adopted both for shared memory systems and for distributed memory systems. DVM high level model allows not only to decrease cost of parallel program development but provides unified formalized base for supporting Run-Time System, debugging, performance analyzing and prediction.

Languages and compilers. As distinct from HPF standard the goal of full automation of computation parallelization and the common data access synchronization is not assumed in DVM system. Using high-level specifications, a programmer has full control of parallel program performance.

Unified parallel model is built in C and Fortran 77 language on the base of the constructions that are "transparent" for standard compilers that allows to have single version of the program for sequential and parallel execution. C-DVM and Fortran DVM compilers translate DVM-program in C or Fortran 77 program correspondently, including parallel execution Run-Time Support system calls. So only requirement to a parallel system is availability of C and Fortran 77 compilers.

Execution and debugging technics. Unified parallel model allows to have unified Run-Time Support system for both languages and, as result, unified system of debugging, performance analyzing and prediction. There are following modes of DVM-program execution and debugging:

• Sequential execution and debugging using standard C and Fortran 77 compiler tools.
• Pseudo-parallel execution and debugging on work station (WINDOWS and UNIX environment).
• Parallel execution and debugging on parallel computer.

Following debugging modes are provided in pseudo-parallel and parallel execution modes:

• automatic verification of parallel directive correctness;
• tracing and comparing the results of parallel and sequential execution;
• accumulation and visualization of data trace;
• performance information accumulation and parallel execution performance prediction.

2 Language overview

2.1 Programming model and model of parallelism

C-DVM language is an extension of ANSI-C language with annotations named DVM-directives. The directives are implemented as parameters of

DVM(<directive>)

macro, which in sequential program is expanded to empty string.

DVM-directives may be conditionally divided on three subsets:

• Data distribution directives (sections 4);
• Computation distribution directives (sections 5, 7);
• Remote data specifications (section 6).

DVM model of parallelism is based on specific form of data parallelism called SPMD (Single Program, Multiple Data). In this model all the processors concerned execute the same program, but each processor performs its own subset of statements in accordance with the data distribution.

In DVM model at first a user defines multidimensional arrangement of virtual processors, which sections data and computations will be mapped on. The section can be varied from the whole processor arrangement up to a single processor.

Then the arrays to be distributed over processors (distributed data) are determined. These arrays are specified by data mapping directives (section 4). The other variables (distributed by default) are mapped by one copy per each processor (replicated data). A value of replicated variable must be the same on all the processors concerned. Single exception of this rule is variables in parallel loop (section 5.1.3 and 5.1.4).

Data mapping defines a set of local or own variables for each processor. A set of own variables determines the rule of own computations: the processor assigns the values to its own variables only.

DVM model defines two levels of parallelism:

• data parallelism;
• task parallelism.

Data parallelism is implemented by distribution of tightly enclosed loop iterations over the processors of the processor arrangement (or the arrangement sections) (see section 5). The loop iteration is executed on one processor entirely. The statements located outside of the parallel loop are executed according to the rule of own computations (see section 5.2).

Task parallelism is implemented by the distribution of data and computations over disjoined sections of processor arrangement (see section 7).

When calculating the value of own variable, the processor may need in values of both own and other (remote) variables. All remote variables must be specified in remote data access directives (see section 6).

2.2 Syntax of DVM-directives

The syntax of DVM-directives is described using a Backus-Nour grammar and the following notations:

Syntax of the directive.

Constraints:

• Specification-directives (descriptive directives) must preceed C declarations of data arrays or DVM-objects to be distributed.
• Executable-directives (executable directives) must preceed C statements (or semicolon - that is empty statement).

3 Virtual processor arrangements. PROCESSORS directive

The PROCESSORS directive declares one or more rectangular virtual processor arrangements on the current set of real processors.

Syntax.

It is possible to define several virtual processor arrangements of different shape if the number of processors in every arrangement will be equal to the number of real processors. If two virtual processor arrangements have the same shape, then corresponding elements of the arrangements are referred to the same processor. Built-in function NUMBER_OF_PROCESSORS () can be used to determine the number of real processors, provided to a program (or subtask).

Note 1. Processor arrangement should be declared as C-array of void * type.

Note 2. To compile program as sequential it should contain the following line:

#define NUMBER_OF_PROCESSORS()  1

Example 3.1. Description of virtual processor arrangements.

DVM(PROCESSORS)  void  *P[N];
DVM(PROCESSORS)  void  *Q[NUMBER_OF_PROCESSORS()],
		   *R[2][NUMBER_OF_PROCESSORS()/2];

The value N has to be equal to the value of the function NUMBER_OF_PROCESSORS ( ), and both have to be even.

4 Data Mapping

C-DVM supports distribution by blocks (of equal or different size) and distribution via alignment.

4.1 DISTRIBUTE and REDISTRIBUTE directives

Syntax.

Constraints:

• The length of dist-format… list must be equal to the array rank. That is, distribution format must be specified for every dimension.
• The number of distributed dimensions of the array (format is not specified as ‘[]’) has to be less or equal to the number of dimensions of dist-target.
• The array block-array-name in GENBLOCK specification must be one-dimensional integer array, with size equal to the size of corresponding dimension of processor arrangement, and a sum of its element values is equal to the size of distributed dimension;
• dist-directive-stuff can be omitted in DISTRIBUTE directive only. In this case distributed array can be used after REDISTRIBUTE directive execution only.
• The ONTO clause specifies a virtual processor arrangement or its section. If ONTO specification is omitted, then the array is distributed upon the current processors arrangement the program or the subtask.
• NEW specification in REDISTRIBUTE directive means that there is no need to copy old values of elements of array, they will be updated.

Let us consider distribution formats for one dimension of the array (one-dimensional array A[N]) and for one dimension of the processor arrangement (one-dimensional array R[P]). Multi-dimensional distributions are considered in section 4.1.4.

4.1.1 Format BLOCK

An array dimension is distributed succesively by blocks of [N/P] elements. If N is not divisible by P there will be one partially filled block and may be some empty blocks.

Example 4.1. Distribution by format BLOCK.

4.1.2 Format GEN_BLOCK

Distribution by blocks of different sizes allows affecting on processor loading balance for algorithms performing different volume of computations for different parts of data area.

Let NB[P] - be an integer array. The following directive

DVM(DISTRIBUTE [ GENBLOCK(NB) ] ONTO R) float A[N];

splits array A on P blocks. The block i of size NB[i] is mapped on processor R[i].

Here:

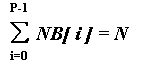
Example 4.2. Distribution by blocks of different size.

4.1.3 WGTBLOCK format

The WGTBLOCK format specifies distribution by blocks according to their relative "weights".

Let WGTBLOCK(WB, NBL) format is specified.

WB(i) defines weight of i-th block for 0£ i £ NBL-1. The blocks are distributed on P processors with balancing of sums of block weights on every processor. The condition

P £ NBL

must be satisfied.

The processor weight is defined as a sum of weights of all the blocks distributed on it . The array dimension is distributed proportionally to processor weights.

BLOCK format is special space of WGTBLOCK(WB,P) format, where WB(i) = 1 for 0£ i £ P-1 and NBL = P.

GENBLOCK format is special case of WGTBLOCK format with some precision.

The example 4.2 can be rewritten using WGTBLOCK format in the following way.

Example 4.3. Distribution by blocks according to weights.

In the example 4.3 P = 4 and distribution is identical to the example 4.2.

As distinct from distribution by non-equal blocks, distribution by WGTBLOCK format can be performed for any number of processors from range 1 £  P £  NBL. For given example the size of processor array R can be varied from 1 to 12.

4.1.4 Format []

Format [] means, that a dimension is not distributed, that is localized on each processor wholly.

4.1.5 Multidimensional distributions

For multidimensional distributions mapping format is specified for each dimension. The following correspondence is established between dimensions of the array to be distributed and the processor arrangement.

Let the processor arrangement has n dimensions. Number the dimensions not formatted as [ ] from left to right d₁, ..., d_k. Then dimension d_i will be mapped on i-th dimension of processor arrangement. The condition k£ n must be satisfied.

Example 4.3. One-dimensional distribution.

Example 4.4. Two-dimensional distribution.

4.2 Multidimensional dynamic arrays

4.2.1 Dynamic arrays in C program

DVM system provides extended features to use dynamic arrays. It allows to create multidimensional arrays which sizes along all dimensions are calculated at runtime. (C language allows this for the first dimension only). Multidimensional arrays of different sizes (and sometimes even of different rank) may be passed as parameters. There are two different ways to deal with multidimensional dynamic arrays in C-DVM language. The first one is based on usage of C-style multidimensional arrays; the second one is to simulate multidimensional arrays using one-dimensional ones.

4.2.2 Using C-style multidimensional arrays

The following discipline of declaration, creation, destruction and usage of multidimensional dynamic array elements is provided:

1. n-dimensional array is declared as a pointer to (n-1)-dimensional array:
   elem_type(*arrid)[dim₂]...[dim_n];
   In particular, a one-dimensional array is declared as a pointer to scalars:
   elem_type *arrid;

2. The array is created by the statement
   arrid=malloc(dim₁*dim₂...* sizeof(elem_type));
   Here:

   elem_type	- element type,
   arrid	- name (identifier) of the array,
   dimi	- size of i-th dimension of the array.

3. Array destruction is performed using free(arrid) statement.

4. Reference to the array element in the program text is denoted as arrid[ind₁]...[ind_n].

The C-DVM compiler translates these constructions to correct descriptions and Run-Time Library calls. But to translate the program as sequential by ordinary C compiler, the sizes of all the array dimensions dim_i (except the first one) must be constants. It is proposed to redefine temporarily them as constants (#define dim_i const …#undef dim_i). The converter removes these redefinitions, more precisely, moves them to the file beginning. Of course, actual ("calculated" in variables) dimensions in case of sequential execution must be equal to selected constant values (see example of Red-black SOR program in Appendix 1).

Example of declaration.

DVM(DISTRIBUTE [BLOCK][BLOCK]) float (*C)[N]; 
/* two-dimensional distributed array */

4.2.3 Simulation of multidimensional arrays via one-dimensional ones

To operate with multidimensional dynamic arrays in C language other method is used. Memory area (one-dimensional) of required size is created and multidimensional array is simulated by macros arrid(ind1,...,indn) similar to Fortran notation. The macros calculates position of element with specified indexes in the memory area, assigned to the array.

C-DVM converter supports this method also. The array is

• described as pointer (to scalars);
• created by arrid=malloc(dim₁*dim₂...*sizeof(elem_type)) statement,
• deleted by free(arrid) statement,
• references to array elements in form arrid(ind₁,...,ind_n) are recognized by the converter and replaced by corresponding construction of RTL DVM.

Example of array declaration (one-dimensional for sequential execution and two-dimensional for parallel execution) and references to its elements:

int Cdim2; /* The second dimension of array C */
DVM (DISTRIBUTE [BLOCK][]) float *C;
#define C(x,y) C[(x)*Cdim2+(y)]
. . .
C(i,j) = (C(i,j-1)+C(i,j+1))/2; 

4.3 Distributing by aligning

Aligning array A with distributed array B brings in accordance to each element of A an element or a section of array B. When distributing array B the array A will be distributed simultaneously. If element of B is mapped on the processor, then the element of A, corresponding to element B via alignment, will be also mapped on the same processor.

Method of mapping via alignment performs the following two functions.

1. The same distribution of the arrays of the same shape on one processor arrangement does not always guarantee allocation of corresponding elements on the same processor. It forces to specify remote access (see section 6) where it is possible not exist. Only alignment of corresponding elements of the arrays guarantees their allocation on the same processor.
2. Several arrays can be aligned with the same array. Redistribution of one array by REDISTRIBUTE directive will cause corresponding redistribution of the array group.

4.3.1 ALIGN and REALIGN directives

The following directives describe array aligning:

Constraints:

• A length of the align-source… must be equal to the rank of aligned array.
• A length of the align-subscript… must be equal to the rank of base array align-target.
• align-directive-stuff can be omitted in ALIGN directive only. In this case distributed array can be used only after execution of REALIGN directive.

Let the alignment of two arrays is specified by the directive

DVM(ALIGN [d₁]…[d_n] WITH B[ard₁]…[ard_m]) float A[100]…[100];

where:
d_i - specification of i-th dimension of aligned array A,
ard_j - specification of j-th dimension of base array B.

If d_i is specified by integer variable I, one and only one dimension of array B, specified by linear function ard_j = a*I + b must exist. Therefore, the number of array A dimensions, specified by identifiers (align-dummy) must be equal to the number of array B dimensions, specified by the linear function.

Let i-th dimension of array A has the size A_i, and j-th dimension of array B, specified by linear function a*I + b, has the size B_j. Since the parameter I is defined on the value set 0…A_i-1, the following conditions must be satisfied:

b ³ 0; a*(A_i –1)+ b < B_j

If d_i is empty, the i-th dimension of array A will be local on each processor independently from array B distribution (it is analogue of local dimension in DISTRIBUTE directive).

If ard_i is empty, the array A will be replicated along the j-th dimension of the array B (it is analogue of partial replication on the processor arrangement).

If ard_i = int-expr, the array A is aligned with the section of the array B.

Example 4.7. Aligning arrays

DVM(DISTRIBUTE [BLOCK][BLOCK]) float B[10][10];
DVM(DISTRIBUTE [BLOCK])  float D[20];
/* aligning the vector with the first line of B) */
DVM(ALIGN [i]  WITH  B[1][i] )   float A[10];
/* replication of the vector aligning it with each line */
DVM(ALIGN [i]  WITH  B[][i]) float F[10];
/* collaps: each matrix column corresponds to the vector element */
DVM(ALIGN [][i]  WITH  D[i]) float C[20][20];
/* alignment using stretching */
DVM(ALIGN [i]  WITH  D[2*i]) float E[10];
/* alignment using rotation and stretching */
DVM(ALIGN [i][j]  WITH  C[2*j][2*i] ) float H[10,10];

Let the sequence of alignments A f1 B f2 C, be specified; f2 be the alignment of the array B with the array C , and f1 be the alignment of the array A with the array B. The arrays A and B are considered as aligned with array C by definition. The array B is aligned by function f2 directly and array A is aligned by composite function f1(f2) indirectly. Therefore applying REALIGN directive to the array B does not cause redistribution of array A.

Generally a set of ALIGN specifications is a set of trees. At that every tree root must be distributed by DISTRIBUTE or REDISTRIBUTE directives. When REDISTRIBUTE directive is executed, the whole alignment tree is redistributed.

4.3.2 TEMPLATE and CREATE_TEMPLATE directives

If values of linear function a*I + b are beyond base array dimension, it is necessary to define a dummy array - referred to as an alignment template – using the following directive.

Then it is necessary to align both arrays with the template. The template is defined using DISTRIBUTE and REDISTRIBUTE directives. The template elements don't require real memory. They specify the processor the elements of aligned arrays must be mapped on.

Consider the following example.

Example 4.8. Aligning with template.

DVM(DISTRIBUTE [BLOCK]; TEMPLATE[102])  void * TABC;
DVM(ALIGN B[i] WITH TABC[i])  float B[100];
DVM(ALIGN A[i] WITH TABC[i+1])  float A[100];
DVM(ALIGN C[i] WITH TABC[i+2])  float C[100];
.   .   .
	DO(i ,1, 98,1)
		A[i] = C[i-1] + B[i+1];

If the sizes of template (and of arrays) are unknown statically the following executable directive should be used:

Example 4.9. Aligning dynamic arrays with template.

DVM(DISTRIBUTE [BLOCK]; TEMPLATE ) void *TABC;
DVM(ALIGN B[i] WITH TABC[i])  float *B;
DVM(ALIGN A[i] WITH TABC[i+1])  float *A;
DVM(ALIGN C[i] WITH TABC[i+2])  float *C;
int N;
.   .   .
N= ... /* size calculation */...;
DVM(CREATE_TEMPLATE TABC[N]);
A=malloc(N*sizeof(float)); 
B=malloc(N*sizeof(float));
C=malloc(N*sizeof(float));
.   .   .
DO(i ,1, N-2,1)
	A[i] = C[i-1] + B[i+1];

4.4 Undistributed data

If DISTRIBUTE or ALIGN directive is not specified for the data, then the data are allocated on each processor (full replication). The same distribution can be specified by DISTRIBUTE directive with ‘[]’ format for each dimension. But in this case access to the data will be less effective.